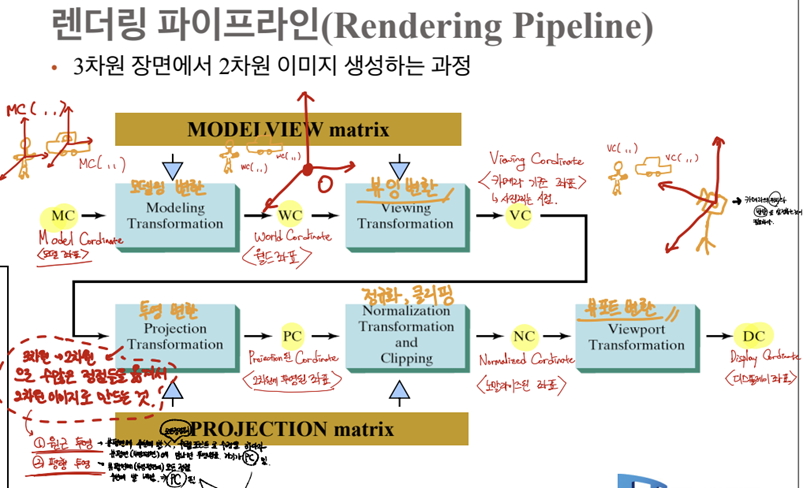
* 투영변환(Projection Transformations) - 주어진 뷰 볼륨의 크기를 -1에서 1 사이의 크기로 만드는 이 과정이 투영과 관련된 변환과정이다.
* 평행투영 - 뷰평면(투영평면)에 모든 정점이 그대로 수선의 발을 내려 투영시키는 방법이다. 뷰 볼륨이 직육면체이다. 원근감의 개념이 없다. 현실에서는 원근감이 없을 수 없기 때문에 평행투영은 현실과 다른 가상의 투영방식이다.
* 원근투영 - 원근감이 반영된 투영방식으로, 3차원 공간의 모든 정점(vc)들을 수렴 포인트로 수렴을 시키다가 수렴 전에 뷰 평면(투영평면)으로 투영시키는 방법이다. pc(투영좌표)이다. (projection coordinate)
* 원근 투영 에서, 동차좌표에서 벡터는 마지막 좌표 0을 가지고, 정점은 마지막 좌표 "0이 아닌 수" 를 가진다.
동차좌표에서 정점 (4,6,2)와 (2,3,1), (6,9,3)은 같은 의미를 가지고 있는 점이다. 마지막 좌표를 1로 만들었을때 같으면 같은 점이라 본다.
* 실제 투영을 할때는 3차원 공간의 모든 정점 p(x,y,z)이 카메라(카메라 점)로 수렴을 하고, 그 사이에 있는 뷰 평면에 투영이 되는 방식이다.


* (왼쪽모델) 카메라 – 원점 / 보라색 관측 평면(뷰평면) - Z near(= Z p) / 원래 3차원 점 – P / 투영된 점 - P’
* (오른쪽) 순서대로 왼쪽 모델을 위에서 아래로 내려본 것
* 알고있는 점 P를 가지고 P’을 유도해 보겠다.
① 비례식 2개 (( Z near : X p = Z : X )) // (( Z near : Y p = Z : Y )) 나옴.
② P’(Xp,Yp,Zp) 를 비례식을 이용해 대체한다.
((투영점은 뷰평면의 z값과 3차원공간의 좌표(x,y,z)를 알고 있으면 계산할 수 있다.))
③ 동차좌표계에서 마지막 좌표를 1로 만들었을때 같으면 같은 점이라 보므로, -Z를 모든 좌표 요소에 곱한다.
((-Z를 곱하는 이유는 오른손좌표계에서 왼손좌표계로 바꿔주기 위함이다. – 우리가 화면으로 보게 될 뷰평면에서 멀어질수록 z좌표가 커지도록 만들기 위함이다.))
④ 이 좌표를 행렬 곱으로 표현하면 그림상 4번의 행렬두개로 표현할 수 있다.
-> 역순으로, 3차원점 P 에 [4번행렬]을 곱해주면 3번 좌표가 나오고, 마지막 원소를 1로 만들면 투영점 P’이다.
* 투영까진 완료했지만 정규화 과정이 남아있다. 즉 투영점 P’(Xp,Yp,Zp)에서 모든 원소가 -1 ~ 1 사이에 있도록 해야
한다.
* Xp, Yp, Zp를 하나 하나 -1 ~ 1사이로 바꿀 것이다.

① 먼저 z 좌표부터 옮긴다. 깊이 정보의 정규화란, z 좌표를 -1에서 1사이로 정규화 시키겠다는 의미이다.
아까 투영점 계산 행렬인 [4번행렬]에서 Z좌표에 영향을미치는 부분은 위 그림에서 a, b 이다.
((즉 a, b를 바꿔야 z정규화가 가능하다))
② 투영변환 전의 원래 뷰 볼륨 안의 3차원점 P(X,Y,Z)에서, Z값이 Z near였다면 정규화 후엔 -1이, Z값이 Z far였다면 정규화 후엔 1이 되어 있어야 할 것이다. 그 정보로 연립방정식을 풀어보면 Z정규화 후 행렬인 M persp 행렬이 나온다.
* M persp 행렬의 의미는, 3차원점 P(X,Y,Z)좌표가 주어졌을 때, X,Y는 가까운 쪽 뷰평면(Z=Znear평면)으로 투영시킨 Xp, Yp를 구하는 것이고, 이때 Z는 가까운쪽 평면(Z=Znear평면)에 투영시킴과 동시에 이 Z값을 -1~1사이로 정규화까지 시킨것이다.

* 투영된 X값, 투영된 Y값도 -1~1사이로 정규화를 시켜야 한다.
* X, Y 각 범위를 -1~1 으로, 즉 길이를 2로 만들어주기 위해서 크기변환 행렬(M scale)을 2 / (X max – X min) 와 2 / (Y max – Y min)를 이용해서 제작한다. (이때 Z는 이미 정규화 완료이므로 영향 안받게 1로 넣어놓음 )
* X, Y의 길이만 맞추는 것으로 각 범위를 -1~1로 만들 수는 없다. -0.5~1.5 이런식일 수도 있다. 하지만, 현재 케이스에서 이렇게 해도 되는 이유는 투영변환을 하기 전의 좌표는 VC로, (Viewing Coordinate) 모든 정점들이 카메라 기준으로 해석되어 있으며, 원근투영의 경우
